Задача по обоснованию оптимальной площади складов на предприятии (логистика) (1027-003)

Ссылка на данный материал: Задача по обоснованию оптимальной площади складов на предприятии (логистика). Номер задачи – 1027-003. Версия 01. [Электронный ресурс]. Разработка Интернет-версии: Горяинов А.Н., 2018. (режим доступа – www.logistics-gr.com )

Задача

Грузооборот склада за год  — 150 тыс. т;

период поступления материалов  — 365 сут;

средняя масса одной партии  — 455 т;

средний срок хранения  — 10 сут;

допустимая нагрузка на 1 м² площади склада  — 1 т;

стоимость содержания 1 м² склада  — 10 руб.;

потери от отказа в приеме груза  — 500 руб/сут.

Под заявкой понимаем партию груза, поступающую на склад. Обслуживание заключается в хранении груза на складе. Аппарат обслуживания — складская ячейка, площадь ячейки 455 м², поток заявок простейший.

Найти оптимальную площадь склада. 

Решение:

1. Определим интенсивность (плотность) потока заявок, партий в сутки:

2. Вычислим интенсивность обслуживания:

3. Рассчитаем площадь склада, необходимую для работы при регулярном поступлении и выдаче груза. Если работа склада и движение через него материальных ресурсов были бы регулярными, то есть детерминированными, полезная площадь склада составила бы, м²:

,           (4)

где  — число оборотов за год:

            (5)

Отсюда следует, что

 м²           (6)

При площади ячейки 455 м2 для работы склада в детерминированном режиме достаточно 9 ячеек (4110 : 455). Однако на практике материальные ресурсы поступают на склад стихийно, поэтому необходимо иметь резерв складской площади.

4. Используем формулу Эрланга

,

где  — вероятности состояния системы  (  — вероятность того, что все аппараты обслуживания свободны;  — занят один аппарат;  — занято два аппарата;  — занято  аппаратов;  — заняты все  аппараты обслуживания или вероятность отказа в обслуживании);  — плотность потока заявок;  — величина, обратная среднему времени обслуживания одной заявки (интенсивность обслуживания).

По формуле Эрланга рассчитаем вероятность отказа в приеме груза на склад при различном числе ячеек начиная с  = 10. Для 10 ячеек формула принимает вид:

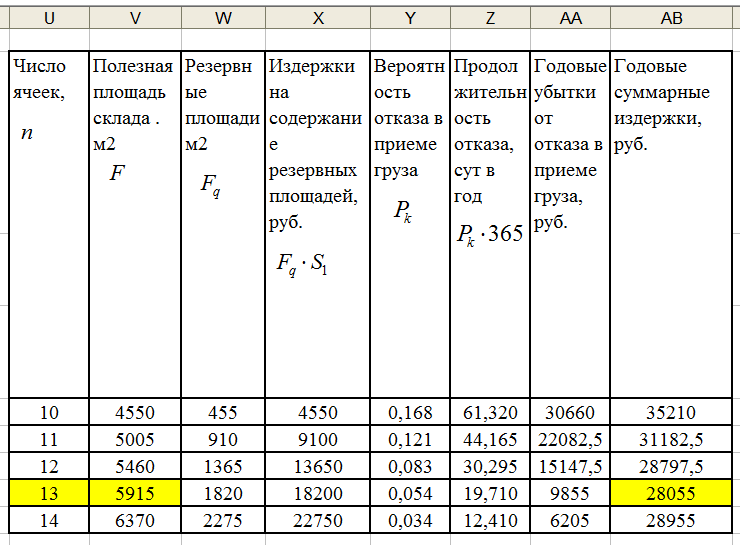
Аналогично определим значения . Полученные данные запишем в таблицу 28.

Таблица 28. Результаты расчета вероятности отказа в приеме груза для складов различной площади

5. Определим полезную площадь склада с учетом дополнительных ячеек, м²:

и т. д.

Результаты расчетов также запишем в таблицу 28.

С увеличением складской площади вероятность отказа в приеме груза будет уменьшаться. Однако увеличение складской площади требует дополнительных затрат. Поэтому обоснованный вывод об оптимальном размере складской площади можно сделать на основании сопоставления расходов на содержание склада и потерь, вызванных отказом в приеме груза.

6. Определим издержки на содержание дополнительной площади склада , потери от отказа в приеме грузов () и общие потери (), руб.:

Для числа ячеек 10

Результаты расчетов занесем в таблицу 29.

Таблица 29. Результаты расчета издержек для складов различной площади

Анализ полученных данных показывает, что оптимальная полезная складская площадь в рассматриваемом случае — 5915 м². При этом суммарные издержки на содержание резервной складской площади и от убытков при отказе в приеме грузов будут минимальными.

Следует обосновать мероприятия, которые позволили бы повысить эффективность работы склада.

Вспомогательные материалы

Файл расчетов в Excel

Тесты

1. Как увеличение числа ячеек на складе влияет на вероятность отказа в приеме груза:

А) Вероятность отказа в приеме груза уменьшается.

Б) Вероятность отказа в приеме груза увеличивается.

В) Вероятность отказа в приеме груза может уменьшаться и увеличиваться (могут иметь оптимум).

2. Как изменение числа ячеек на складе влияет на годовые суммарные издержки:

А) Годовые суммарные издержки могут уменьшаться и увеличиваться (могут иметь оптимум).

Б) Годовые суммарные издержки увеличиваются.

В) Годовые суммарные издержки уменьшаются.

Источники:

1. Ворожейкина Т. М., Игнатов В. Д. Логистика в АПК. — М.: КолосС, 2007. — С. 161-166 (184 с.)